フィルター挿入による焦点位置の移動
カメラの前にフィルターを挿入することによる焦点位置の移動について考えます.
キーワード
- フィルター
- 焦点位置移動
- 球面収差
今回のポイント
- カメラの前にフィルターを挿入すると焦点位置はカメラ側にズレる.
- カメラの前にフィルターを挿入すると球面収差が発生する.
- 厚さ
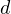 のフィルターをカメラの前に挿入するとF/#が大きい(8以上)の望遠鏡では,焦点位置はカメラ側に約
のフィルターをカメラの前に挿入するとF/#が大きい(8以上)の望遠鏡では,焦点位置はカメラ側に約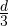 ほどズレる
ほどズレる - 厚さ
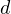 のフィルターをカメラの前に挿入するとF/#が小さい(8未満)の望遠鏡では,球面収差の影響が大きく,焦点位置はカメラ側に約
のフィルターをカメラの前に挿入するとF/#が小さい(8未満)の望遠鏡では,球面収差の影響が大きく,焦点位置はカメラ側に約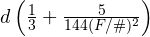 ほどズレる
ほどズレる
焦点位置がずれる方向
冷却CCDカメラではカメラの前にフィルターを挟んで撮影を行うことがあります.実はこの場合はフィルターの影響により焦点位置がずれるため,接続リングの光路長を適切に設定しなくてはいけません.今回はこのことについて考えてみます.
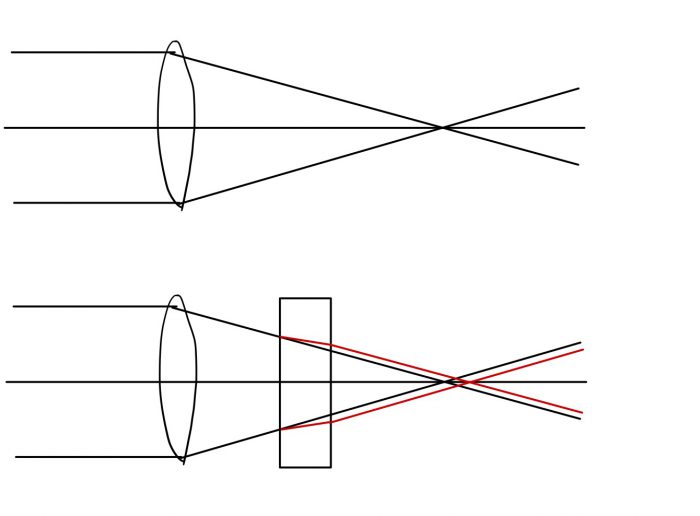
通常フィルターはガラスで出来ており,その屈折率はおおよそ1.5程度です.空気の屈折率はほぼ1であるため,図1のように光は空気からフィルターに入るところと,フィルターから空気に出るところで2回屈折し,焦点位置がカメラ側に移動します.
焦点位置のズレの大きさ
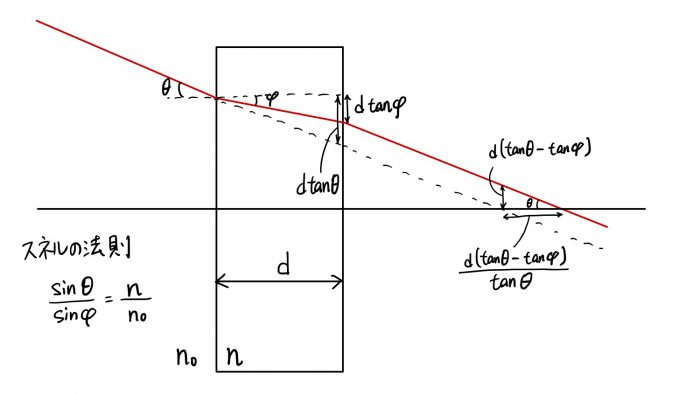
フィルターの部分に注目してみます:
一般的に考えるため,フィルターの外の屈折率を![]() ,フィルターの屈折率を
,フィルターの屈折率を![]() として
として![]() の場合について考えています.
の場合について考えています.
図から分かるようにフィルターを挟むことで焦点位置がカメラ側に![]() だけ移動しています.スネルの法則
だけ移動しています.スネルの法則![]() を用いると:
を用いると:
(1) 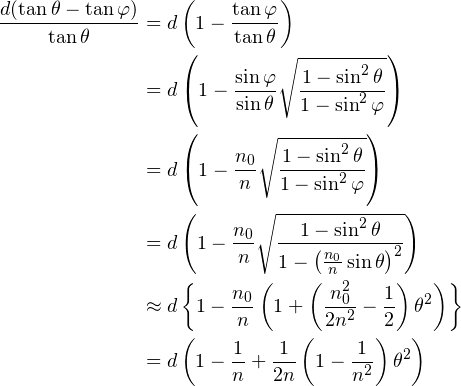
と計算出来ます.4行目から5行目に移る際に![]() の3次の項まで残す近似を行い,5行目から6行目に移る際は空気の屈折率
の3次の項まで残す近似を行い,5行目から6行目に移る際は空気の屈折率![]() を代入しました.
を代入しました.
この計算から分かることは,入射角![]() でフィルターに入射した光線はフィルターがない時に比べてカメラ側に
でフィルターに入射した光線はフィルターがない時に比べてカメラ側に![]() だけずれた場所に焦点を結ぶということです.また,焦点位置がずれる量はフィルターの挿入位置に無関係なことも分かります.これはフィルターから射出される光線の角度はフィルターに入射する光線の角度と等しいためです.
だけずれた場所に焦点を結ぶということです.また,焦点位置がずれる量はフィルターの挿入位置に無関係なことも分かります.これはフィルターから射出される光線の角度はフィルターに入射する光線の角度と等しいためです.
暗い望遠鏡の場合(F/# > 8)
F/#が8以上の光学系であれば,![]() を十分小さいと考えて(1)式を近似することにより次の結果を得ます:
を十分小さいと考えて(1)式を近似することにより次の結果を得ます:
(2) ![]()
ただし![]() としました.
としました.
したがってF/#が8以上の望遠鏡であれば,カメラと望遠鏡の間の長さをフィルターがない時に対して![]() だけ増やしてあげれば良いことになります.
だけ増やしてあげれば良いことになります.
明るい望遠鏡の場合 (F/# < 8)
一方F/#が8未満の望遠鏡では入射角![]() が大きくもなるため(2)式の近似が出来ません.そのため(1)式がそのまま焦点位置のズレということになります.
が大きくもなるため(2)式の近似が出来ません.そのため(1)式がそのまま焦点位置のズレということになります.
(3) ![]()
ただし![]() としました.
としました.
(3)式は![]() によって焦点位置が異なることを意味しています.特に
によって焦点位置が異なることを意味しています.特に![]() が大きい時は焦点位置はカメラ側にさらに寄ることになります.
が大きい時は焦点位置はカメラ側にさらに寄ることになります.
図3:焦点位置のズレ
この![]() の違いによる焦点位置のズレのことを「球面収差」といいます.
の違いによる焦点位置のズレのことを「球面収差」といいます.
この球面収差のために,光線が一点に収束することがなく,どうやっても星が少し大きさを持ってボケたように写ってしまいます.光束が一番細くなっている部分を最小錯乱円といい,CCDの面をその最小錯乱円に合わせるようにすれば星が一番小さく(シャープに)写ります.計算の詳細は割愛しますが,フィルターの屈折率が![]() の場合,フィルター無しの場合の焦点位置に対して最小錯乱円の位置は次の式で与えられることが知られています:
の場合,フィルター無しの場合の焦点位置に対して最小錯乱円の位置は次の式で与えられることが知られています:
(4) ![]()
繰り返しになりますが,この最小錯乱円の位置およびその大きさ(星像の大きさ)はフィルターの挿入位置に依りません.そのため,フィルターとカメラの距離は気にする必要はありません.
具体的な例としてε-180ED望遠鏡(F/#=2.8)と厚さ![]() mmのフィルターを使っている場合を考えましょう.この場合(4)式へ代入して約
mmのフィルターを使っている場合を考えましょう.この場合(4)式へ代入して約![]() mmが得られます.つまり,最小錯乱円の位置がフィルターが無い時の焦点位置に対して
mmが得られます.つまり,最小錯乱円の位置がフィルターが無い時の焦点位置に対して![]() mmだけカメラ側に寄るので,アダプターの長さを調整して望遠鏡とCCDの距離を (バックフォーカス)+
mmだけカメラ側に寄るので,アダプターの長さを調整して望遠鏡とCCDの距離を (バックフォーカス)+![]() mmにすればOKです.
mmにすればOKです.
自分の望遠鏡のF/#と使っているフィルターの厚みに合わせてこれらの数値を計算し,正しい位置にCCD面を持ってくるようにしましょう.


最近のコメント