ノイズの計算 Part 2
コンポジットやビニングを行うとS/Nが変化する.このカラクリについて詳しく説明します part 2
キーワード
- 誤差の伝播
- コンポジット
- ビニング
まとめ
- 誤差の伝播の式
- コンポジットの意義
- ビニングの意義
Part 1では円柱の体積を求める例を使って誤差の伝播の式を説明した.
今回は誤差の伝播の式を天体写真の場合に使うことで,コンポジットやビニングの意義について理解する.
CCD/CMOSの各ピクセルのカウント値にはノイズが含まれている.
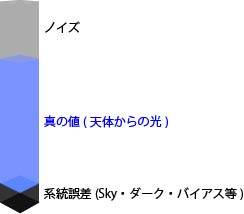 このノイズはカメラの性能とは無関係に偶然誤差として発生し,原理的に取り除けないものであった.
このノイズはカメラの性能とは無関係に偶然誤差として発生し,原理的に取り除けないものであった.
(ここでは簡単のため系統誤差は既に十分取り除かれているものとする)
天体写真ではコンポジットによって各フレームの対応するピクセル同士を
- 加算する ⇔ 加算コンポジット
- 平均値を求める ⇔ 加算平均コンポジット
という操作をしている.
これによってS/Nが向上する.
天体写真のノイズに関して実際に誤差の伝播の式を使ってコンポジットがどう影響を与えるのか見てみます.
誤差の伝播の式をもう一度書いておこう.
誤差の伝播,
,
,・・・の測定値から計算の結果
の値が求まる場合を考えます. 数式で書くと関数
を用いて
と書ける状況です. このとき
,
,
,・・・のそれぞれの測定値が標準偏差
,
,
,・・・を持っている場合,計算結果の
の持つ標準偏差
は以下で求まります:
(1)
(これは変数,
,
,・・・間には相関が無い場合の公式である.天体写真に関する限りほとんどの状況でこの式で十分である.)
加算コンポジット
![]() 枚の画像を加算コンポジットする場合を考える.
枚の画像を加算コンポジットする場合を考える.
つまり「![]() 枚の画像の対応するピクセルのカウント値を足し上げる」
枚の画像の対応するピクセルのカウント値を足し上げる」
という操作を考える.
ある特定のピクセルに着目し,そのピクセルの![]() 枚目のカウント値が
枚目のカウント値が![]() ,その標準偏差が
,その標準偏差が![]() だとします.
だとします.
加算コンポジット後の合計カウント値を![]() ,その標準偏差を
,その標準偏差を![]() と置くと
と置くと
(2) ![]()
の関係が分かります.この式中の各![]() はそれぞれノイズを含んでいるので,合計された
はそれぞれノイズを含んでいるので,合計された![]() もノイズを含んでいるはずです.この
もノイズを含んでいるはずです.この![]() のノイズがコンポジット後のノイズです.
のノイズがコンポジット後のノイズです.
誤差の伝播の公式(1)に当てはめ,このコンポジット後のノイズを求めてみると,
(3) 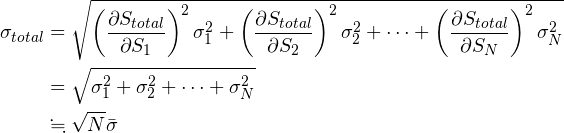
ただし各![]() の平均値
の平均値![]() としました.
としました.
これを見ると![]() 枚を加算コンポジットするとノイズは
枚を加算コンポジットするとノイズは
(4) ![]()
となり増える事が分かる.
一方![]() は
は![]() 枚加算したことにより
枚加算したことにより
(5) ![]()
となり単純に![]() 倍になった.
倍になった.
(6) ![]()
ただし![]() は平均値
は平均値![]() です.
です.
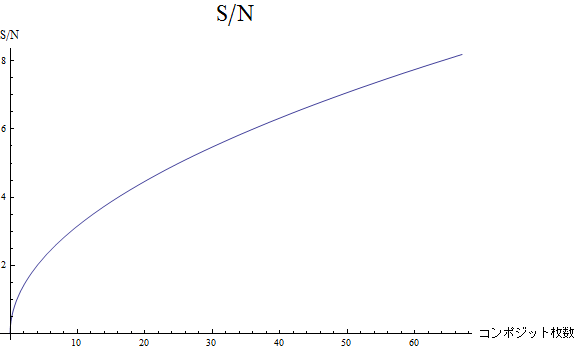
S/Nを計算してみると
(7) 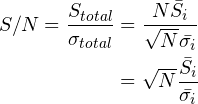
となっていて,![]() 枚コンポジットすると一枚のS/Nよりも
枚コンポジットすると一枚のS/Nよりも![]() 倍良くなる事が分かります.コンポジットの意義はここにあります.
倍良くなる事が分かります.コンポジットの意義はここにあります.

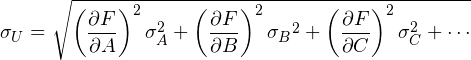
最近のコメント