コンポジットの意義
ここではコンポジットを行うと何がどうなるのか?何故良いのかを説明します.
キーワード
- コンポジット
- ショットノイズ
- S/N
- 撮影枚数,露出時間
まとめ
- コンポジットでS/Nは向上
- S/Nの伸び方はだんだん鈍る
- S/Nは√(撮影枚数)に比例して伸びる
「コンポジット」とは?
「コンポジットとは同じ天体を撮影した複数の画像を位置合わせをした後に加算もしくは加算平均して一枚の画像を作ること」です.
(ちなみに天文学者はコンポジットとは言わずにスタックと言います.)
コンポジットを行うとコンポジットをする前に比べて![]() が向上します.皆さん経験的にこのことを理解してらっしゃると思います.ではなぜ
が向上します.皆さん経験的にこのことを理解してらっしゃると思います.ではなぜ![]() が向上するのでしょうか?
が向上するのでしょうか?
まずは百聞は一見にしかずということで,コンポジットによりS/Nがどうなるのかシュミレーションをお見せしましょう.
簡単のため一様な明るさのものをn枚撮影した画像を加算平均にてコンポジットした場合のシュミレーションを作りました.
CCD/CMOSの各ピクセルに電子が溜まっている様子を考えてください.各直方体の高さがそれぞれのピクセルのカウント値を表します.
スライダーを動かしてもらうと,コンポジット枚数nが増えるに従ってだんだんとガタガタだった画像が滑らかになっていく様子が分かると思います.ぐるぐる回してみることもできますよ!
(動作にはWolframCDFという無料プラグインが必要です.ブラウザによっては動かないかもしれません.Firefox ver.49では動きました)
動かない方のためにシュミレーションのGIFアニメものせておきます.
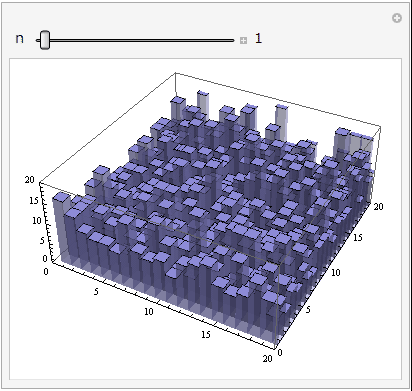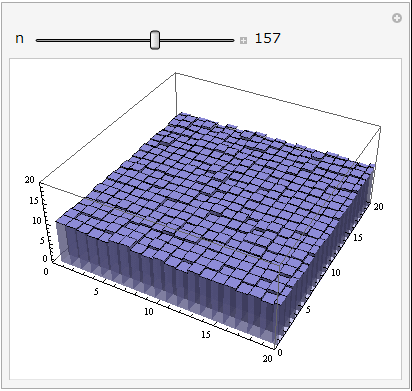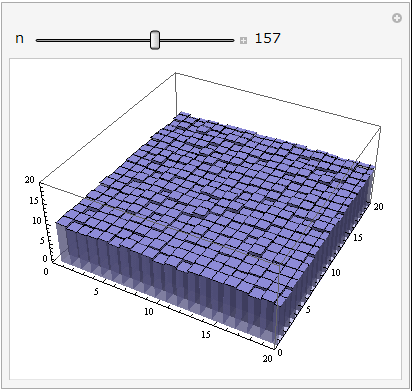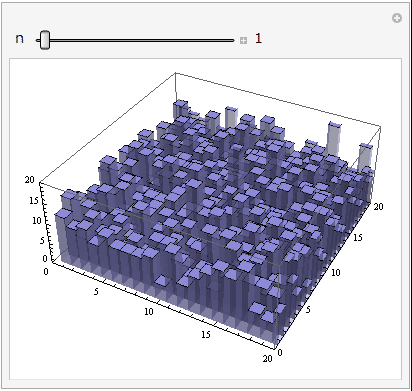
見てもらうとコンポジット枚数nが増えると加算平均コンポジット後の画像がどんどん滑らかになっていくのが分かります.加算平均ですのでシグナル![]() の大きさはコンポジットをしても変わりませんが,ノイズ
の大きさはコンポジットをしても変わりませんが,ノイズ![]() の大きさがどんどん小さくなっていきます.結果としてコンポジット後の画像の
の大きさがどんどん小さくなっていきます.結果としてコンポジット後の画像の![]() は向上し,滑らかになっています.
は向上し,滑らかになっています.
天体写真で重要なショットノイズの場合はシグナル![]() とノイズ
とノイズ![]() の間に
の間に![]() の関係があるため,
の関係があるため,![]() となります.これはつまり
となります.これはつまり![]() は露出時間のルートもしくは撮影枚数のルートに比例して良くなっていくということです.
は露出時間のルートもしくは撮影枚数のルートに比例して良くなっていくということです.
(1) 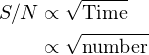
これをグラフにしてみると以下のようになります
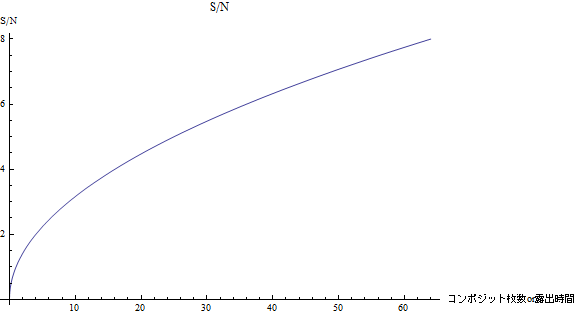
グラフからコンポジット枚数を増やすと![]() が向上していきますが,その伸びはだんだんと鈍くなっていくことが分かります.
が向上していきますが,その伸びはだんだんと鈍くなっていくことが分かります.
例えばコンポジット枚数を2枚→8枚と増やすと![]() は
は![]() 倍に向上しますが,64枚→70枚と増やしても
倍に向上しますが,64枚→70枚と増やしても![]() は
は![]() 倍にしかなりません.同じ6枚増やすのでも違うのです.
倍にしかなりません.同じ6枚増やすのでも違うのです.
たまに聞く話として「ダークのコンポジットでは64枚以上増やしてもあまり関係ない」というものがありますが,これはこのような事情を考えての発言と理解出来ます.
(もちろんコンポジット枚数を増やせば確実に![]() は向上するわけですが,撮影の労力と効果を考えると64枚程度で十分?という話なのだと思われます.例えば64枚からさらに
は向上するわけですが,撮影の労力と効果を考えると64枚程度で十分?という話なのだと思われます.例えば64枚からさらに![]() を2倍に上げようと思うと64×4=256枚撮影する必要があります...)
を2倍に上げようと思うと64×4=256枚撮影する必要があります...)
ここでは加算平均コンポジットの場合で考えましたが,加算コンポジットの場合でも![]() は全く同じに向上していきます.
は全く同じに向上していきます.
どうしてコンポジットをすると![]() が向上するのか?より詳しく知りたい方は「ノイズの数学」の項を参照してください.
が向上するのか?より詳しく知りたい方は「ノイズの数学」の項を参照してください.

最近のコメント